
Lyftkraft? Förklara hellre med isflak än Bernoulli!

Nedsvepningsfältet bakom en Cessna Citation VI, visualiserat i en molnöversida. De fullt utvecklade virvlarna ligger 9 meter rakt under den plats flygplanet befann sig på 15 sekunder tidigare. Paul Bowen fotograferade och Cessna ställde bilden till förfogande.

Det finns en klar likhet mellan att flyga och att "jumpa" från isflak till isflak. Jumparen kan endast hålla sig uppe genom att hela tiden accelerera nya is- och vattenmassor nedåt. En illustration av Torgil Rosenberg.
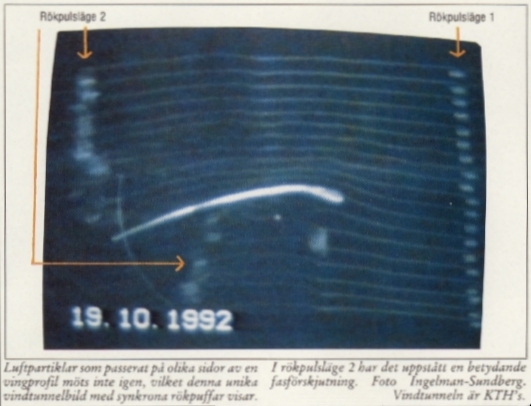
Luftpartiklar som passerat på olika sidor av en vingprofil möts inte igen, vilket denna unika vindtunnelbild med synkrona rökpuffar visar. I rökpulsläge 2 har det uppstått en betydande fasförskjutning. Foto Ingelman-Sundberg. Vindtunneln är KTH´s.
Piloter kommer aldrig att förstå hur farliga "svallvågorna" efter stora flygplan är, så länge de inte får veta hur lyftkraft verkligen skapas.
av Martin Ingelman-Sundberg
Goebbels: Om en lögn upprepas tillräckligt många gånger blir den upphöjd till sanning.
Miljoner piloter lever bokstavligt talat på en lögn. I flygskolan har de fått lära sig att vingar lyfter för att luftens hastighetsökning på översidan skapar undertryck. En sådan beskrivning strider mot grundläggande fysikaliska lagar. Det riktiga är att tryckändringar, som ger lyft, kommer från tröghetskrafter i luftmassan som påverkas av vingen under färden framåt. Jämför gärna med att ta sig fram på vatten jumpande på isflak.
Den gängse beskrivningen kunde möjligtvis betraktas som en harmlös skenbar förenkling, tills det började komma larmrapporter om svallvågor efter stora trafikflygplan. Idag är det en internationell skandal att myndigheterna fortsätter att föreskriva flygteori som bygger på en feltolkning av Bernoullis lag.
Varför ska piloter lära sig flygteori?
Alla småbarn lär sig genom ackumulerad praktisk erfarenhet av sig själva att gå, utan att veta ett dugg om balans, tyngdpunkter, tröghet mm. Det fungerar ganska bra. Kanske halkar de på isgata på vintern och slår sig litet, men de lär sig successivt vad som gör ont. Ingen hjälpinstruktion utifrån behövs. Det finns kanske numera i våra gener. Liknande är det för vuxna som vill åka skridsko på spolad bana på mark. De riskerar bara att slå sig.
Helt annorlunda blir det för den som vill vidga åkningen till dess möjliga gränser, på sjöis. Då kan redan den första kontakten med svag is och kallt vatten medföra att den nya erfarenheten aldrig mer behöver utnyttjas. Istället är det praktiskt att via "teori" lära sig var de dödliga gränserna går.
Att piloter bör ges förståelse för hur deras flygplansvingar fungerar har liknande motivering.
Syftet med teoriundervisning för piloter är att ge dem en kunskap med vars hjälp de inför oförutsedda och aldrig övade situationer ska kunna handla på bästa sätt. Förutsättningen är att det som utlärts varit fysikaliskt korrekt. Annars är undervisningen meningslös.
Reaktionskrafter
Fram till mitten av 1930-talet beskrev flygfolk lyftkraften på ett övergripande och fysikaliskt korrekt sätt, med att vingarna accelererar luftmassa nedåt, varvid reaktionen mot luftens tröghet gav lyftkraften. Den felaktiga Bernoulli-tolkningen började också komma med, men fick inte stå ensam, som idag. Att vingen "puffar till" (= sätter igång rörelsen nedåt av) successivt nya luftmassor var också bröderna Wright medvetna om. Lilienthal hade 1895 i detalj beskrivit hur under- och övertrycken runt vingprofilen uppstår genom centrifugalkrafter på luftmasseelementen, som av vingen tvingades röra sig i krökta banor. Centrifugalkraft har folk lätt att förstå och faktum är att denna beskrivning motsvarar trots enkelheten utmärkt vår tids modernaste beräkningsmetoder, som möjliggjorts av superdatorerna.
I litet mera vetenskapliga ordalag kan det sammanfattas som att lokala tryckändringar initieras av att en kropps fasta yta tvingar passerande tröga luftpartiklar att ändra sina momentana rörelseriktningar. De därav initierade tryckändringarna påverkar sekundärt också den lokala hastigheten längs med rörelsebanan, varefter i tredje hand tryckändringen förstärks på grund av ökade centrifugalkrafter vid samma banradie.
Denna växelverkan är också orsaken till att sänkningen av trycket ovanför en lyftande profil, på grund av den högre farten, blir absolut sett större än stegringen under densamma, där ju hastigheten minskat p g a det där rådande högre trycket.
Trots att pionjärerna alltså kunde beskriva det principiella lyftkraftsskapandet fysikaliskt korrekt, så kunde de dock inte beräkna tryckets storlek och fördelning mellan vingens över- och undersida. Detta blev roten till framtida missförstånd.
Daniel Bernoulli (1700-1782) professor i matematik och medicin, publicerade 1738 i sin bok "Hydrodynamica" bl a grundläggande experiment och slutsatser om sambandet mellan tryck och rörelseenergi för vatten som strömmade ut ur hål i vertikala kanaler. Eftersom rörelseenergin är en funktion av både massan och hastigheten ger detta också ett samband mellan trycket och hastigheten.
Matematiskt trick orsakade flygets livslögn
Leonard von Euler (1707-1783) matematiker och vän med Bernoulli, uppställde grundläggande ekvationer för hur en fluid borde strömma omkring en kropp, varvid han utgick från balansen mellan tröghetskrafter och tryckkrafter på varje enskilt litet fluidelement. Eulers ekvationer var dock under två sekler omöjliga att lösa och utnyttja, förutom i ett viktigt specialfall: "ett icke kompressibelt fluidmasseelements rörelse längs en rak linje". Det samband mellan rörelseenergi per volymenhet och lokalt tryck som Euler fick fram för detta specialfall motsvarade det som Bernoulli studerat, varför von Euler lär ha givit det namnet "Bernoullis ekvation". Bernoulli själv jämför även vattnets rörelser med en under tyngdkraftens inverkan fritt fallande kropp.
Bernoulli själv har aldrig skrivit "att hastighetsökning orsakar trycksänkning", vilket påstås i den av luftfartens tillsynsmyndigheter föreskrivna pilotutbildningen. Tvärtom har han direkt påpekat att detta är ett olämpligt påstående, medan "att trycksänkning orsakar hastighetsökning" är acceptabelt att säga.
Genom att införa den förenklande förutsättningen "absolut inkompressibilitet" kunde man behandla hela strömningsfältet med en matematisk teknik med en ren så kallad hastighetspotential. Denna teknik bygger på vissa matematiska "verktyg" som källor, sänkor och virvlar (cirkulation) vilka endast simulerar inducerade hastigheter. Tekniken möjliggjorde att om man i förväg på experimentell grund fastställde utströmningsriktningen från vingbakkanten så kunde man beräkna de lokala hastigheterna i hela fältet runt vingen. Detta t o m utan datorer.
Sedan hastighetsfältet beräknats, möjliggjorde ett diagnostiskt "omvänt" utnyttjande av Bernoulli-ekvationen bestämning av vad trycket måste vara i aktuell punkt för att fluidens tröga massa där ska ha nått den pre-dikterade hastigheten. De tidiga teoretikernas medvetande om det omvända Bernoulli-användandet verkar dock senare ha glömts bort även bland många strömningsprofessorer.
Detta, själva slutledet i potentialteoriberäkningarna, är vad som gett upphov till hela luftfartsvärldens, inklusive ICAO, beklagliga missuppfattning om att Bernoullis lag skulle säga "att hastighetsökning orsakar trycksänkning" och som kommit att snedvrida all utbildning. Sedan har det felaktiga grundpåståendet kombinerats med en hel serie fysikaliskt helt felaktiga exempel för att påvisa påståendets riktighet. Och ovanpå detta lika felaktiga argument och exempel på varför hastigheten ska bli hög, så att det felaktiga påståendet kan tillämpas.
Så här skapar flygplan sin lyftkraft
På omslaget till FLYING, mars 1992, visades ett foto som kan ersätta många timmar flygteori. Det kan sägas visualisera själva grundprincipen för flygning enligt system tyngre än luft. Och det gör det inte i en liten vindtunnel utan uppe i den verkliga flygmiljön. Bilden borde ha sin plats i teorisalen i varenda flygskola.
En Cessna Citation kommer stigande upp ur molnen ovanför Lake Tahoe i Californien. I aktertornet till en gammal B-25 Mitchell, som flyger 500 meter framför, sitter fotografen Paul Bowen. Även när Cessnan kommit helt ovanför molnet så tvingar den luften nedåt, så att molnöversidan blir först badkars-formad, för att 15 sekunder efter passagen ha rullats ihop till två koncentrerade virvlar, vilka rör sig nedåt med ett konstant inbördes avstånd.
Kontinuerligt avstamp från successivt nya massor av luft
För att hålla flygplanet i luften, mot jordens dragningskraft, måste planets vingar kontinuerligt accelerera en viss del av den luft som passeras i motsatt riktning, dvs nedåt, så att denna luft sedan vingen just passerat har fått en viss hastighet nedåt.
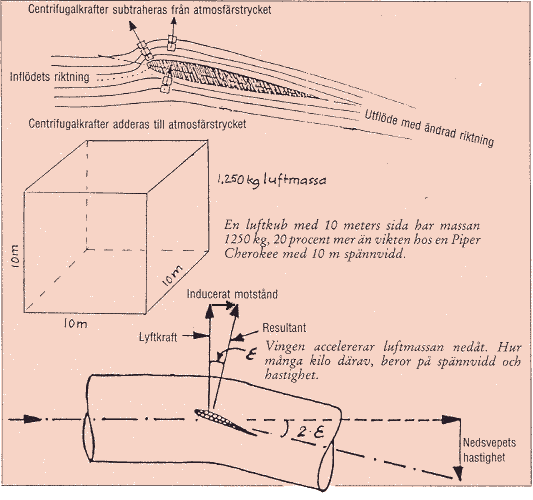
Den luften har massa (mäts i kg). En kub luft med samma sida som spännvidden på ett typiskt sportflygplan innehåller 1250 kg luftmassa vid marktryck. En tänkt luftcylinder med Cessna Citations spännvidd både som diameter och längd innehåller på höjden 6000 fot en massa av inte mindre än 3,5 ton (!) och den har dessutom en motsvarande tröghet. Trögheten gör att den inte frivilligt ändrar sitt initiala vilotillstånd när vingens "anfall" tvingar den att flytta sig undan nedåt. Detta motsvarar den så kallade Newtons Första Lag. Luften kommer därför enligt Newtons Tredje Lag att utöva precis lika stor motkraft mot vingen (dvs lyftkraft) som erfordras för dess massinnehålls successiva acceleration nedåt.
Denna sker genom att det uppstår en sänkning av luftens tryck mot vingens översida, vars begränsningsyta ju "flyr undan" nedåt från den stillastående atmosfärsluften. En del av atmosfärstrycket balanseras då av de tröghetskrafter som måste övervinnas för att ge luften fart nedåt i riktning mot ytan, vilket innebär att de subtraheras från trycket mot ytan. Vingens undersida "tränger sig" nedåt, varför tröghetskrafterna adderas så att trycket mot denna blir ökat. Som resultat uppstår den tryckdifferens mellan över- och undersidorna som ger själva lyftkraften.
Varje sekund kan man säga att Citation-vingen "tar avstamp från" (=aktiverar) så mycket luft som ryms i en cylinder med samma diameter som flygplanets spännvidd och med längden = den sträcka som flygplanet förflyttar sig under en sekund. Avstampet sker dock successivt under vingpassagen.
Storleken på denna "ekvivalenta aktiverade massa" framkom redan för 75 år sedan som ett resultat av en utförlig beräkning som professor Ludvig Prandtl gjorde så snart han utformat sin s k virvelteori för vingberäkning. Om vingens lyftkraftsfördelning i spännviddsled avviker från den därvid optimalt angivna, så motsvarar det att den aktiverade massan (tvärsnittet därav) blir något reducerad, vilket ger ökat "lyft"motstånd. Sambandet gäller oförändrat idag och virvelteorin är fortfarande den mest använda beräkningsmetoden.
Det finns en direkt likhet även med att jumpa på isflak, där man tar avstamp från successivt nya is- och vattenmassor vilka accelereras nedåt. Det är också samma princip som utnyttjas när man genom att vinkla ut ett roder vid en vingbakkant med detta ger luftmassan en extra acceleration uppåt eller nedåt just innan den lämnar vingen.
Svallrörelserna
Omedelbart när vingen passerat så har nämnda luftmassa lämnats av med en viss hastighet nedåt. Den rörelseenergi som tillförts återvinns aldrig. Denna energiförlust är vad som orsakar det så kallade (lyft)inducerade motståndet. Det rör sig inte alls om någon liten lokal omströmning från tryck- till sugsida runt själva vingspetsen, som det brukar sägas. Om det ska kallas "läckage" så sker det både långt ovanför, under och utanför spetsarna.
Uttrycket att läckaget orsakar inducerade motståndet kommer från en jämförelse med en tänkt oändligt lång vinge. Denna skulle nämligen inte behöva orsaka någon kvarstående nedåthastighet, varför det lyftinducerade motståndet skulle bli noll. Vi ska här inte fördjupa oss i detta, eller hur i detalj vingens profil fungerar. Bara konstatera att det fysikaliskt viktiga fenomenet för vingprofilens funktion är att undersidans luftström inte förmår följa ytan runt bakkanten utan släpper från ytan, samtidigt som strömningen runt framkanten och ovanför förblir anliggande.
I det aktuella Citation-fallet (spännvidd 15,9 m, vikt 6700 kg, fart 175 knop/87 m/s) passerar vingen varje sekund genom en cylinder innehållande 18,4 ton luft. Den tröga massan hos all denna luft bibringas successivt en nedåthastighet av 3,7 m/s.
Närmast bakom planet syns att molnöversidan huvudsakligen tvingats iväg nedåt. Längre bak, dvs en viss tid efter passagen, har annan luft från sidorna hunnit strömma in ovanför den initialt nedsvepta luften och likaså har luften nedanför tvingats ut åt sidorna. Successivt har de två motroterande virvlarna bildats. Deras virvelcentra stabiliseras på ett inbördes avstånd av 79 procent av vingens spännvidd (Prandtl). Deras avstånd i bilden är därför 12,6 m, vilket kan utnyttjas till att ge en längdskala i detta tvärsnitt.
Det kan beräknas att virvelcentra på fotot ligger cirka 9 meter under den höjd där vingen verkligen passerade då den initierade luftens rörelse nedåt. Jämför gärna utvecklingen av virvlarna i vattenytan efter ett paddeltag, det är samma sak.
För vingar med stor utsträckning i längdled relativt spännvidden, exempelvis Draken och Viggen, hinner de virvlar som orsakas av vingens främre delar ofta att koncentreras redan ovanför vingens egna bakre delar.
Hur länge lever de?
Med ledning av flygplanets tyngd, spännvidd och fart och med aktuell lufttäthet går det att beräkna virvlarnas styrka och därmed den periferihastighet som råder på olika radier från centrum. Den är i detta fall 15,4 m/s 0,5 m från virvelns centrum.
Cessna Citation har ganska låg vikt per meter spännvidd och flyger här någorlunda fort, varför dessa virvlar är relativt ofarliga. Om dess fart sänks till hälften dubbleras virvelstyrkan. En Concorde med vikten 185 ton inom 26 meters spännvidd, skulle vid nu aktuell fart ge virvlar som är mycket farliga för mindre flygplan, 17 gånger så starka som Citation! En 747 - 15 gånger, DC-9 - 5 gånger och Piper Cherokee 0,25 gånger så starka.
Den som kanske erfarit kyttet när han eller hon med sin Cherokee i brant sväng korsat sina egna virvlar, kan tänka sig detta kytt 60 gånger starkare. Så blir det att flyga in i lyftkraftsvirvlarna, eller svallvågorna, efter en långsamt flygande 747.
I USA har t o m ett totalhaveri skett då en DC-9 under skolflygning i samband med landningen kom för nära efter en 747 och kastades över på rygg och gick i marken.
Tiden det tar innan virvlarna dämpats ut och övergått i oordnad turbulens beror på atmosfärens egen turbulens. I stilla luft varar de längst och det kan vara en fråga om många minuter innan de dämpats i väsentlig grad. Innan vidden av detta problem till fullo insågs hann USA för 25 år sedan förlora sin prototyp till överljudsbombplanet B-70, då ett eskorterande jaktplan greps av dess virvlar och kolliderade med det.
Det vanligen använda uttrycket vingspetsvirvlar ger en bedrägligt mild association, även om det är samma sak som åsyftas.
Martin Ingelman-Sundberg har i fyra år stridit för att lyftkraft ska beskrivas korrekt i teoriundervisningen för piloter. Men de som har makten att rätta till reglerna för utformningen av läromedel och examina tar antingen inte hans kunskap på allvar, eller inser inte allvaret i att fortsätta lura ett helt pilotkollektiv. Det skulle vara intressant att veta vilket, gärna presenterat av tillträdande flygsäkerhetschefen på Luftfartsinspektionen.
Ingelman-Sundberg är nu pensionerad efter 40 år som yrkesaerodynamiker, varav 30 som chef för sektionen för låghastighetsaerodynamik vid Flygtekniska Försöksanstalten. Flyger gör han fortfarande, med certifikat erövrat för 54 år sedan.
Newtons lagar:
Lag l definierar begreppet en massas tröghet, dvs att om den inte påverkas av någon yttre kraft så bibehåller den sitt initiala tillstånd av rörelse eller vila.
Lag 2 anger hur stor kraft som erfordras för att ändra tillståndet, dvs att accelerera massan i någon riktning. Den kallas också den allmänna kraftekvationen.
Lag 3 säger att om en kropp A påverkar en kropp B med en viss kraft, så påverkar också kropp B kropp A med exakt samma kraft.
Källförteckning
Tidskrift
Ingelman-Sundberg, Martin, Lyftkraft? Förklara hellre med isflak än Bernoulli! MACH, MACH 56 (nr 1, 1994), s 43-45.